When is technology risky?
Many failures are easy to explain. When a door plug falls off of a 737 Max and opens a big hole in the plane, it’s clear how the accident itself went down, even if there may be hard questions about the context and how to ensure it doesn't happen again.
But sometimes it's hard to understand how a failure even happened. The other 737 Max crisis—the one that caused two deadly plane crashes in 2019—was a long chain of minor software and communication failures:1
The Max’s aerodynamics were different from the original 737’s in some stall conditions. So Boeing added new software that would automatically adjust controls in a way that translated a pilot’s actions to the same outcomes as in the 737, even if the underlying inputs were different. (This was important so airlines wouldn't have to retrain pilots on the new plane, which would be expensive.)
Boeing didn't tell pilots about this change, because the point of that system was to keep the user experience the same, and because stalls shouldn't occur anyway.
But a sensor failed and erroneously activated the stall-mitigating system, pointing the plane toward the ground. (The sensor failure seems to have been noticed a couple days earlier, but inspectors let the plane continue flying under business pressures.) Furthermore, a standard warning system to alert pilots to different readings from different sensors was never installed.
Even without knowing what the system was or how it worked, it could be fixed by shutting off the automatic stabilizers, the same way other issues are solved. But the (relatively inexperienced) pilots didn't do this, nor did they take other precautions like turning back early or flying higher.
An unrelated safety system kicked in to prevent the plane from heading toward the ground, but this combined with the first system to speed the plane up until the second was overpowered and couldn’t prevent a crash.
The accumulation of controls, sensors, and changing hardware has made modern airplanes complex systems: each component affects the performance of the plane in hard-to-understand ways, so a failure anywhere can have rapidly cascading effects. More and more disruptions across domains have that sort of cause today. (In other words, the world is getting weirder.) That's for two reasons: 1) through experience, we've learned how to engineer away a lot of simple failures; planes sometimes broke in midair a half-century ago, but we're shocked when it happens today. And 2) by introducing technology that makes systems faster and more interconnected, we're making complex failures more likely.
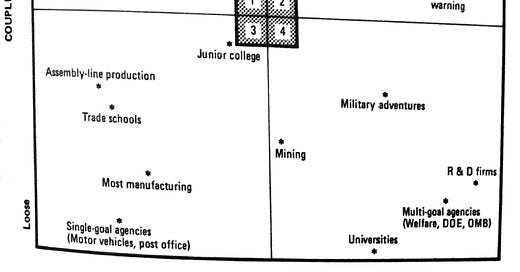
Complex systems research is usually quite theoretical, studying common patterns across fields like neuroscience, ecology, and finance. Normal Accidents, written in 1984 by sociologist Charles Perrow, is instead a book about applied complexity. His inspiration was an assignment by a federal commission to study Three Mile Island from a social science perspective. His contribution is exactly two characteristics that he says define risky complex systems: nonlinear interactions and tight coupling. And most of his book is built around the applied social scientist's favorite tool—a single 2x2 matrix—where he methodically goes through a bunch of major industries and sees where they fit.
Opaque interactions and tight coupling have exploded in the intervening four decades, and even more is coming in the AI age. But when it comes to the risk posed by such systems, things may not be as hopeless as Perrow thought.
The complexity matrix
Before you can define what a high-risk system is, there's the annoying step of defining what a system itself is. Systems are usually composed of sub-systems, which are composed of units, which are composed of parts, but those are arbitrary distinctions – an airplane is itself a system, but it's also a unit in the larger air traffic control system. Perrow, appropriately, doesn't dwell on this ambiguity; as long as you can break it down into those parts, you can call it a system. Accidents take down at least a sub-system; anything below that level is just an incident.
This book is about a specific type of accident: a system accident, in which multiple failures interact in unpredictable or unexpected ways (like the software-affected 737 Max crash). This is in contrast to component failure accidents, in which one thing breaks severely (like the door-plug 737 Max crash).
Even in nuclear plants, Perrow's go-to example of a complex system, he says only about 10% of accidents are system accidents; most are still component failures. So why are they worth writing a whole book about? Plenty of engineers are already writing about how to avoid component failures; system accidents are much less well-understood, so we need a new theory for them.
Two things characterize systems in which such accidents are most likely. First, they have nonlinear interactions.2 By definition, any large system has lots of interactions, but they're usually easy to understand: assembly lines are set up so the output of one step is directly used by the next step. But sometimes—either inevitably or by poor design—interactions are not so obvious:
One component serves multiple functions. In a chemical plant, one machine may both absorb heat from a reaction and use that energy to heat up something else. If it fails, one area isn't getting enough heat and another is overheating; if you focus on mitigating one of those effects during a crisis, you'll miss the other.
Unrelated components are near each other. In one oil tanker accident, the engine room was located next to the tank holding the oil, which sprung a leak. When that caused a fire, workers looked for all the usual causes of an engine fire and tried to fight it correspondingly; they didn't expect it could be an oil fire, so their efforts just spread the flames further.
Information isn't measured directly. There's no sensor for how much coolant is in a nuclear reactor (it's dangerous to put anything not strictly necessary in there), so it has to be inferred from other sources; those are more likely to be misleading, especially if something else has gone wrong.
In all of these cases, when something goes wrong, it's hard to figure out what happened. That's especially problematic when the system also has the second characteristic: tight coupling, meaning that what happens in one part of the system strongly and rapidly affects others. Common archetypes of tight coupling include:
There's only one way to do things. Baking a cake is tightly coupled; it'll come out differently if you do steps out of order or make any substitutions. (In contrast, many manufactured goods contain modular components that can be made in parallel and swapped out for others with different materials or designs.)
Everything happens all at once. You can't stop a chemical reaction mid-stream and then finish it later; you can't stop a glassmaking project mid-stream, cool it down, and reheat it again when you're ready.
There are no spare parts. This might be for physical reasons (NASA can't put too many backups into a rocket because it would be too heavy to fly), or because a component is so integrated that it can't feasibly be swapped out if it's broken.
Perrow maps a couple dozen industries on this matrix. Dams are very tightly coupled—once a dam has a significant leak, it's almost impossible to stop, and everything downstream will quickly be ruined—but they’re highly linear; it’s clear how they’re supposed to work, and accidents are usually the result of unheeded warnings or sloppy behavior. Universities are nonlinear—good luck figuring out what effect the president's new directive will have when the deans might disagree with the president, the faculty might disagree with the dean, and the students might disagree with everybody —but they’re loosely coupled because everything takes forever.
What can you do if you’re in the top right—a nonlinear, tightly coupled system? Traditionally, to prevent accidents you add safety features: an alarm that tells you something is wrong, a button for someone to stop it, or a machine to fix things automatically. These won't prevent the initial failure, but they'll stop it from spreading to the larger system.
Those work fine for linear systems, but they’re insufficient in complex systems. For one thing, you just need a lot more alarms and controls: if you shut off one unit, you need to monitor everything else it touches to make sure nothing else goes wrong. So nuclear plant control panels are extremely dense, which is great for visual gags in The Simpsons, but hard for real people to manage. Failures in complex systems, including Three Mile Island, are often ascribed to "operator error," but that's because operators are put in an impossible position (and, says Perrow with the smugness of a sociology professor, probably because of class bias among investigators).
For another, safety features themselves can fail or turn on when they're not supposed to. This is even worse than not having one in the first place, because it presents second-order problems that are bound to be unfamiliar: see the first 737 Max crash, or a Crystal River nuclear plant accident in 1980, when some controls short-circuited and made the coolant appear colder than it was, triggering an automatic response system that overheated the reactor.
So safety features can't make complex systems truly safe; the only way to do that is to redesign the system itself.
An arms race of risk
To this point, we've talked about complexity and coupling as innate properties of a system. Sometimes that's the case: it's always going to be easier to decompose car assembly into linear steps than anything that involves a chemical reaction. But complexity and coupling are also design choices—meaning we can make systems less risky by reducing them. For instance, US air traffic control authorities made some changes after dealing with too many near-collisions in the mid-20th century: They mandated that all planes carry transponders (which broadcast their altitude, not just the 2-D coordinates available by radar) to deal with the all-too-common problem of cowboy pilots entering airspace without a flight plan, reducing complexity for controllers to figure out who's where. And they developed "skyways" for long-distance flights, reducing coupling by cutting down the places where planes could conceivably intersect.
Recently, systems are more often trending the other way. Complexity and coupling make systems more efficient and more capable, so we're choosing to do that and live with the risk:
Businesses are making (and customers are choosing) more specialized products. That's great for satisfying specific needs, but it can create weird, nonlinear interactions. When COVID-19 came to the US, people weren't using the bathroom more, but they were staying home more, and the toilet paper supply chain for commercial buildings had become entirely separate from toilet paper for homes. There was a hidden connection between "going to work" and "wiping your butt", so when we stopped going to work, there (temporarily) wasn't enough to meet the new demand at home.
Manufacturing is Perrow's top example of a linear and decoupled system, but that’s changed due to "just-in-time" production processes: to reduce inventory costs, companies supply only as many parts as needed and assemble products as quickly as possible. That makes manufacturing more coupled: in early 2021, a scarcity of trailing-edge semiconductors (costing ~$2 per chip) meant automakers couldn't produce enough cars (worth four orders of magnitude more), because they didn't have much supply saved and they couldn't come up with alternatives.
Technology pushes the envelope further. It’s behind most of those designed increases in complexity and coupling (barcode scanning allows you to price a much wider variety of products; predictive analytics allows you to optimize supplies), and it also creates unintended risk in unplanned ways:
Social media has made politics weirder. Not necessarily in the "misinformation" sense, but in the sense that viral feedback loops mean that public opinion can change rapidly and confusingly. This causes "accidents" that disrupt the status quo, such as in the case of [insert your least favorite right-wing leader and/or left-wing social movement here].
Digitization is removing friction in financial markets, increasing coupling. Historically, if rising interest rates reduced the long-term value of a bank's assets, nobody really noticed or cared. But when Silicon Valley Bank became insolvent in 2023, a) it quickly became common knowledge via VC WhatsApp chats, b) it was easy for companies to move money out digitally, so c) they did, and others had to follow so they wouldn't be the last ones left, taking down SVB.
Technology can also make systems safer; better sensors can make a system appear more linear, and better automated failsafes can reduce coupling. However, in a type of Peltzman effect, system designers often just use that as a license to increase efficiency (and therefore risk) on another dimension. After the skyway system reduced coupling of air traffic control systems, airlines responded by running faster planes with less separation between them, increasing the risk of accidents on the margin again. (In this case the system was still net safer overall, but that doesn't have to happen.)3
That's a natural tendency, because you see the benefit of more efficient systems all the time, whereas you see the benefit of avoiding accidents only rarely (and even then you might not know it). In the immediate wake of the pandemic, businesses and governments showed a lot of interest in investing in "resilience" against crises; a few of those efforts came to fruition, but for the most part we’ve already moved on. When we aren't even managing forest fire risk correctly—the textbook example of taking small steps today to prevent major accidents in the future—it's hard to be optimistic that we can redesign systems to reduce risk at a cost.
If you believe in Perrow’s framework, that's concerning, because complexity and coupling are about to explode in the AI age:
AI systems are very nonlinear—we don't really understand how advanced models work, so we can't predict what will happen if we use them in a new situation.
AI systems are very coupled—the more we allow such systems to act and learn without a human in the loop, the more rapidly any issue can snowball into something bigger.
Should we believe in the framework?
Nuclear risk, revisited
Nuclear power is at the very top-right of Perrow’s risk matrix, and he keeps coming back to it throughout the book. He admits that other upper-right technologies, such as recombinant DNA, can provide a lot of societal value, so we may have to do what we can to mitigate the worst risks and live with what's left. Nuclear power systems, however, "are hopeless and should be abandoned because the inevitable risks outweigh any benefits."
The consensus “intelligentsia” position today is that nuclear power is as safe, if not more so, than other sources of power. What gives?
I can think of three ways to reconcile these positions, with very different implications:
Perrow's framework and analysis are still correct: nuclear power is really risky; it only seems safe because we've gotten lucky so far.
Nuclear power used to be really risky, but now it's not, because we've made it more linear and less coupled. This would make Perrow's analysis of nuclear power’s prospects wrong, but it would validate his 2-by-2 framework, if not even make him a hero for telling us exactly how to fix things.
Nuclear power was never that risky, or it's become less risky for reasons unrelated to complexity and coupling. This is a serious blow to Perrow's framework – if not its accuracy (maybe nonlinearity and coupling don't drive system accidents), then its value (maybe he's right about system accidents, but those are a rounding error in overall risk compared to other accidents, so they're not worth writing about).
Have we just been lucky so far (#1)? The argument is simple: since Normal Accidents was published in 1984, cumulative reactor-hours worldwide have only increased by a factor of four, because we've stopped allowing most new nuclear plants. And in that time, we've had two nuclear accidents that were an order of magnitude worse than anything before them (Chernobyl and Fukushima). Project the long-tailed distribution out further, and it's only a matter of time before we have even worse accidents; they haven't happened already precisely because we realized nuclear energy was hopelessly unsafe.
But it's easy to poke holes. For one thing, the rest of the distribution hasn't followed suit: beneath Chernobyl and Fukushima, there have only been three level 4-6 accidents in the last four decades, compared to 15 in less time before that.
And more to the point, Perrow's prediction was already at odds with the quantitative evidence in 1984: very few people had died from nuclear system accidents, and certainly fewer than many seemingly less risky systems. He justifies this by saying, more or less, just wait, we've been lucky, and look at how many close calls there were. (He continued saying this after Fukushima.) But when we keep being lucky over time, and when the close call rate slows, at some point it becomes less convincing.
He also justifies this by making fun of economists and their cost-benefit analysis, arguing that people have useful heuristics that don't fit that framework: they focus more on tail risks than averages, and they overweight risks to third parties who don't have any control over the system. These are fine arguments in general, but I don't see how they relate to Perrow's 2x2; it seems more like a coincidence that nuclear power both has high complexity/coupling and major tail risks. (For example, Fukushima had the highest disaster potential of any nuclear accident we've seen, and that sure seems like a component failure rather than a system accident.) Perrow insinuates that nonlinear and coupled systems are inherently more likely to affect third parties, but is that true? "Single-goal government agencies" are at the very bottom-left of his chart, and “authorize tests for a new disease” sure sounds like a single-goal agency task, but the CDC’s failure to do so in February 2020 probably led to thousands of third-party deaths.4
Did we redesign nuclear systems to be less coupled and more linear (#2)? On the margin, probably; newer models of reactors rely more on "passive" safety systems that don't have to turn on (e.g., ones that only use gravity), and thus are less likely to be part of compounding failures. But something like half of today's reactors had already been built by 1984, and those haven't blown up yet either. Maybe there have been other system design improvements that have made a huge difference; I'd love to hear them, since this is the most interesting outcome. But I haven't yet found anything that seems meaningful.
Is there a different reason to think nuclear power has become less risky (#3)? Right after Chernobyl, there was a steep drop in the rate of nuclear “incidents”, a measure that includes the big accidents above but also much smaller events. The proximate cause, according to that essay, was an organizational process called Probabilistic Risk Assessment—breaking down the system into every single component and making sure it works as expected.
This is about the least Perrow-like approach imaginable. (He, of course, criticizes the Rasmussen report that first introduced PRA and vastly underestimated meltdown risk as missing the role of complexity.) Perrow says that components will always fail, and you should judge the risk of a system by how those failures compound. But maybe there's a threshold where if component failures are sufficiently unlikely, they'll never compound?5
Maybe that’s not true, and maybe we have just been lucky. Or maybe it’s true for nuclear power, and all the other systems that were around in Perrow’s time, but AI is so much more complex and coupled that it won’t be true then. But it’s in some sense the most hopeful theory: not only is it not impossible to manage system risk, but it can be done merely by the tedious, traditional method of making every component safe.
These bullets describe the first crash (Lion Air in Indonesia); the second one had different details – in particular, pilots had been made aware of the software system – but the same gestalt of interacting software, sensor, and human failures.
Perrow uses "complex interactions" instead of "nonlinear", but he uses "linear interactions" as the opposite, so it means the same thing. I've swapped in "nonlinear" here because I think it's more clear on first read and because "complex" has come on to take other, if mostly similar, connotations when describing systems.
Perrow's passion is organizational design, so in the final chapter he throws in some analysis from this perspective, although it's not at all core to his argument, which is why I'm relegating it to a footnote. He says nonlinear systems should be operated by decentralized organizations (so people on the ground can use their acumen to find non-obvious problems), and tightly coupled systems should be operated by centralized organizations (so everyone can listen to orders and respond quickly in a crisis). This raises a paradox for systems that are both nonlinear and coupled: you can't be both centralized and decentralized at once. This was probably a bit of a stretch even in Perrow’s time, but I mention it here because it's an area where technology really has broken the trade-off: even in decentralized systems, people can now get the information to respond rapidly to a crisis. For example, the "xz backdoor" was found by a decentralized open-source community, but the news of its discovery reached all corners of that community (and well beyond) within hours.
You could argue any system that can unintentionally harm third parties has nonlinear interactions by definition, but then the framework is useless for predicting risk, only for identifying it in retrospect.
I think Perrow’s 1999 afterword about Y2K implicitly admits this. He (wisely) doesn’t make a prediction about whether there will be an accident; he only says that if there are failures, they’ll cause a system accident (e.g., if electric grids go down, then there will be correlated failures in fields like manufacturing where it’s assumed only one thing can go wrong at a time, which will make a lot of other things worse). But nothing meaningfully failed.